|
|
For many projects benefits and costs occur at different times. We need a way of comparing and assessing projects with benefits over different times. A Very Fast Train now would have high capital costs, but operating costs for the next twenty years would be much lower than for the existing line. How do we compare the options of the VFT and upgrading the existing line? We want a photocopier; should we buy an expensive one with a low cost per page, a cheap one with a high cost per page, or no copier at all, taking our copying to a commercial operator down the street?
To do such analysis we need to be able to bring all flows to a common point of time. Most frequently that is the present time - we find the present value of a cash flow (or of a set of benefits or costs which can be brought to dollar amounts). The key analytical concepts we need are:
All of these concepts become clearer when we look at them in more detail. First, a revision of compound interest theory.
Funds, when used to purchase productive assets like a telephone company, produce income. Therefore borrowers pay and lenders or investors receive a return on those funds. The rate of return, whether a return on debt or equity, is generally denoted by the symbol r.(1)
Imagine an investment in which we keep re-investing our money to get the same percentage return. Every year the funds are re-invested, to buy more earning assets.
Using the symbol St to denote the sum we have at time t, and St+1 to denote the amount we have at the next period, we can construct a basic difference equation.
St+1 = St + return
= St + St * r
That's like the population growth model. We can gather terms in our equation, to get:
St+1 = St * (1 + r)
If our funds could earn 7.5 percent, for example, the relationship between one year and the next would be:
St+1 = St * (1 + 0.075)
= St * (1.075)
Imagine we start at time 0, and invest $1000 at 7.5 percent. Then after one year we will have:
S1 = 1000 * (1.075)
After another year it will be:
S2 = S1 * (1.075)
= S0 * (1.075) * (1.075)
= 1000 * (1.075)2
After seven years it will be:
= 1000 * (1.075)7
That superscript is a shorthand way of saying "to the power of".
The general form of compounding equation is:
Sn = S0 * (1 + r)n
A common term for Sn is future value. You may recognize the equation as the familiar compound interest formula. The figure (1 + r)n is known as an accumulation factor; it denotes the accumulation of $1.00 to its future value.
Now calculating a figure like 1000 * (1.075)7 by longhand could put a dent in anyone's leisure or work time. Till around thirty years ago most people relied on compound interest tables. Then it became possible to do such sums by repeated calculations on a desk calculator, while those who had access to a computer could use Fortran, Basic or Cobol programs to solve such problems. Then came programmable calculators and spreadsheets.
Using a spreadsheet for such a problem may sound like using a sledge hammer to crack a peanut, but it has the benefit of allowing us to see what's going on. What's happening at each stage of the process? Where are we at years 1, 2? What happens if I invest at 8.0 percent (but with a higher risk)? What if I draw off $100 after two years? All these are easy to do, changing just one variable at a time.
It's worth remembering that the syntax for compounding, or
exponentiation in most spreadsheets is the symbol ^ (just above
the 6 on the keyboard). Thus, if the interest rate were in the cell B7 and the number of
years were in the cell A12, the formula <=(1 + $B$7)^A12> would give us the growth
factor. (Alternatively you may give the cell B7 a name like <interest>, in which
case the equation becomes <=(1 + interest)^A12>.)
Exercise
We are probably most familiar with the concept of future value when we consider superannuation and saving for retirement.
Develop a model which, starting with your age now, shows how much you will accumulate by retirement at different rates of saving and at different rates of return. Model, say, a saving rate of $5000 a year, and vary the rate of return, r, from 3 percent up to 7 percent. A model of this is at ch09ex01.xls. (See the third spreadsheet for an example of a model with easy variation of a key input.) Note that the figures in Column C are accumulation factors.
We need a technique for bringing future savings, revenues and costs to some present value as a basis of comparison. What is $x in y year's time worth to us now?
To answer this we need to know by how much we discount the future. This in itself is difficult to measure, an issue to which we turn at the end of the chapter.
As a metaphor, imagine that Great Aunt Clarabella has just died, leaving you $5000, and her executors tell you it will take a year to wind up her estate. What is that $5000 in a year's time worth to you now?
If you could get 7 percent on your money, then you would find that present value by solving for x the equation:
5000 = x * (1.07)
That gives x = 4673. The figure 0.07 is called the discount rate, also generally denoted by the symbol r (though some writers use the symbol i). It is the opportunity cost of capital - the opportunity foregone through not having the money now. That is the return (interest, profit or capital gain) we could earn if we had the funds to invest now.
Imagine the executors had said it would take two years. Then we solve the equation:
5000 = x * (1.07) * (1.07)
5000 = x * (1.07)2
x = 1/(1.07)2 * 5000
x = 0.8734 * 5000
x = 4367
That figure 0.8734 is called the discount factor, and is the factor by which we discount a cost, revenue or saving in n years' time, to bring it to present value. It is generated by the equation:
Discount factor = 1/(1 + r)n
This is simply the reciprocal of the accumulation factor.
When we apply discount factors to cash flows in several different periods, we can add up the present values to get a net present value or NPV of the set of cash flows, or of any set of flows which can be expressed in financial terms.
Imagine we are buying a photocopier. We can buy a photocopier for $1 500 which has a cost per sheet of 6.0 cents, or we can buy one for $6 000 which has a cost per sheet of 2.0 cents. Given our volume of copying, we may need to know which to buy, or we may wish to know at what volume the higher priced machine becomes more economical. We are given, by the Department of Finance, a discount rate of 8 percent. We would plan to keep our copier for six years, at which stage we would expect to trade it in for 30 percent of its purchase price. We do 20 000 copies a year. Which one should we buy? Or should we put our copying out to a commercial operator for 8 cents a sheet?
Our objective in this exercise is to choose the least cost option of providing those 20 000 copies a year for the next five years. Therefore we need to find the net present value of the cost of these three options, and choose the option with the lowest NPV.
Our spreadsheet is at ch09ex02.xls, and is set out below. We have included the discount factor as an identified cell. The key calculations are to obtain the discount factors by reference to the discount rate and the year, to multiply the discount factors by the cash flow to get present values (also know as discounted cash flows, DCF) and to add up these present values to get the NPV of the set of cash flows.
Note that we have defined the first year to be year 0. This is conventional in discounting models; we may equally have decided to call the first year 1. Mathematically it would be a little different, but not greatly so. Whatever we do we are approximating a continuous flow by a lumpy set of figures; we will use the photocopier every day, not just at the beginning of each year as the model implies. This approximation will not change our decision rules for the vast majority of projects. (For funds managers, however, handling large amounts of money, precise timing is crucial, and they may use daily or even half day models, as when investing in the overnight money market.)
Note, too, the distinction between the discount rate (8%) and the discount factors (which are driven by the discount rate, and differ each year). Note the distinction between present value (each year's outlay discounted) and the net present value (the sum of these present values).
| Discount rate | 8% | Photocopier Outlays | |||||||||
| Number of sheets | 20 000 | ||||||||||
| Copier 1 | Copier 2 | No copier | |||||||||
| Year | Discount factor | Purchase disposal | Copies | Net outlay | Present value | Purchase disposal | Copies | Net outlay | Present value | Copies | Present value |
| 0 | 1.0000 | 1500 | 1200 | 2700 | 2700 | 6000 | 400 | 6400 | 6400 | 1600 | 1600 |
| 1 | 0.9259 | 1200 | 1200 | 1111 | 400 | 400 | 370 | 1600 | 1481 | ||
| 2 | 0.8573 | 1200 | 1200 | 1029 | 400 | 400 | 343 | 1600 | 1372 | ||
| 3 | 0.7938 | 1200 | 1200 | 953 | 400 | 400 | 318 | 1600 | 1270 | ||
| 4 | 0.7350 | 1200 | 1200 | 882 | 400 | 400 | 294 | 1600 | 1176 | ||
| 5 | 0.6806 | -450 | 1200 | 750 | 510 | -1800 | 400 | -1400 | -953 | 1600 | 1089 |
| NPV | 7185 | NPV | 6772 | NPV | 7988 | ||||||
This shows that the net present value of the cost of the
three options are:
Cheaper copier 7 185
Expensive copier 6 772
No copier 7 988
This gives a preference for the expensive copier, with a low cost per page. A way of interpreting the figures is that if we outlaid $7 185 now, and spent some of this on buying the copier, some on copies as needed, and let the balance accumulate interest at 8 percent, then we would exactly finance the operation. And so on with the other two options.
Here it is worth mentioning the uses and abuses of forward estimates. They should not be used for evaluation. If we had been looking simply at cash outlays over four years we would have found that the cheaper copier would have involved far less cash outlay. This is an example of why we should not use forward estimates, which are no more than cash projections, for comparative purposes.
We should, of course, subject our model to sensitivity analysis. What if we do only 15 000 copies a year (buy the cheaper copier), if only 10 000 copies (no copier)? What if our discount rate rises to 10 percent (no change in decision). We should also look at the effect of varying the discount rate. At lower discount rates the expensive copier continues to dominate; at higher rates the cheaper copier dominates, and at very high rates it's best to have no copier. These zones are shown in the graph over the page. As a general rule low discount rates favor investments with a high ratio of up-front to running cost, and as the discount rate rises we are willing to incur high ongoing costs in the future in favor of lower outlays now. (To generate a graph similar to this you will need to use the Data Table function in Excel.)
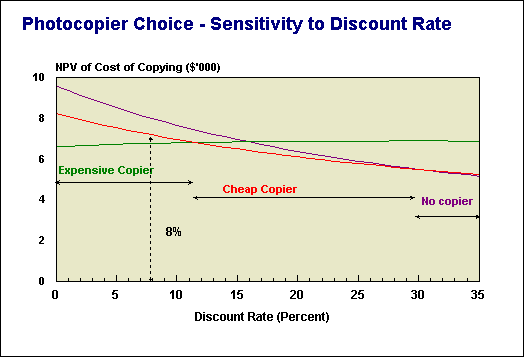
This sort of decision is common in the public sector. We have little choice about whether to undertake an activity or not; we need therefore to find the lowest cost means possible to achieve a given outcome. (It is a form of cost-effectiveness analysis, in answer to the question "what is the lowest way of financing a given number of copies?".) In more commercial situations, where we can put a price on our output, we follow the fundamental rule of benefit-cost analysis, and select the project with the highest net value.
DCF analysis is a standard technique, even for minor decisions (e.g. down to $1000) in the private sector. It is used in the public sector, but its use is confined mainly to large projects. There is no reason for not using it, however; the reasons it is not used seem to be a lack of familiarity with the technique and often an undue obsession with immediate cash outlays.
DCF analysis is a fundamental tool in benefit-cost analysis, except in the cases where costs and benefits occur all in the same year. Sometimes discounting is done on the costs and benefits separately; that is, a NPV of costs is determined, and a NPV of benefits is determined, and the two are compared. The NPV following such a manipulation is no different from the NPV of net cash flows, in which costs and benefits are offset before discounting. Finding the NPVs of the two streams, however, does allow for calculation of benefit-cost ratios, and an illustration of this technique is given in the next chapter.
Also, although the term "discounted cash flow" is used, this is more to describe a technique rather than to imply that the costs and benefits have to correspond to actual cash outlays or receipts. In the private sector projects can usually be evaluated simply by considering the cash flows. In the public sector, however, while costs and benefits may be tangible and measurable in dollar terms, there is often no cash flow. In a transport model we would include travel time savings, for example, as if these were actual cash benefits to the users concerned, although there would never be any cash transaction. Similarly, if our project involved some loss of environmental amenity, we would try to put a dollar value on this, occurring as an outlay, even though we never make the transaction. Restricting our analysis to actual cash flows is to restrict our evaluation to a financial evaluation; public policy should rest on economic evaluation. (This distinction is drawn out more fully in Chapter 8.)
Exercise
The Shire of Wanton Valley (a tax exempt organization) wants to put up a 35 bed private nursing home. It must be an economically justifiable project.
The revenue per resident it will get is $20 000 a year, and there will be no trouble filling it. The shire can plan on all beds being full and earning money once construction is completed, which should take about a year.
The architect has presented two options:
The first has a low construction cost ($1.4 million). Its running costs will be $430 000 a year once completed and occupied. It is a conventional building.
The second is a higher cost option ($2.3 million). Its running costs, however, will be $130 000 a year lower, as it will incorporate solar energy systems, low maintenance materials, a layout to make for easier cleaning, and a kitchen with significant labor savings.
Demographic projections suggest that in eight years time the north coast may have become yuppified. So in the interests of conservatism the Council's projections are going out no more than eight years from construction, which will take a year. At the end of the eight year period the cheaper building would have no value, but the other building would have a disposal value (for conversion to a motel) of $200 000.(2) The projected cash flows in $'000 are:
| Year | Option 1 | Option 2 | ||
| Outlay | Revenue | Outlay | Revenue | |
| 0 | 1 400 | 0 | 2 300 | 0 |
| 1 to 8 | 430 | 700 | 300 | 700 |
| 8 (disposal) | 0 | 200 | ||
The real cost of capital (the opportunity cost on other
projects) is 5 percent. What is your advice to the shire? A spreadsheet is at ch09ex03.xls. By now you will be finding the mechanics of
developing spreadsheets easy; the hard part often comes in explaining your assumptions in
developing spreadsheets and why you have used a particular discount rate or time horizon.
As an example of the type of conflict that may occur over discount rates, imagine an accountant on the council points out that the shire has more good projects than money, because the state government has capped their borrowing capacity. They are knocking back projects, such as local roads and drainage, with rates of return up to 10 percent because of this shortage. If you have verified the accountant's information, would your advice change? These are issues in capital rationing, to be taken up in Chapter 10.
There are no hard and fast rules on choice of a time
horizon. If a project could have a limited life, then a short time horizon may be wise.
For long life infrastructure projects, such as power lines, freeways, ports, where there
is little risk of technological obsolescence, then time horizons up to thirty years or
more may be justified. In practice, however, the sorts of discount rates used in
government (5 to 12 percent) suppress long term costs and benefits so heavily that little
is lost in the choice between, say 25 and 30 years. What is important, however, is to
ensure that mutually exclusive projects are evaluated using the same time horizons. Where
you know different projects will have different lifetimes, you will need either to force
fit a common time cycle (e.g. by defining the longer life project to have a certain
residual value, or by using life cycle costing, a technique we
cover in Chapter 13.
You will have noticed that we have been laboriously laying out our spreadsheets, with a column for the years, a column for the discount factors, and a column for the present values. But, you may note, computers and calculators have built in functions which allow us to obtain the net present value with a single function.
We set the models out to give us some idea of their workings, to help us understand what elements are important, and which are trivial. Also, at times, the bottom line answer from a mathematical function may be misleading.
For example, one measure, sometimes used in project ranking, is the internal rate of return (IRR). That is the value of r which sets the NPV exactly to zero. The exercise below is an example of the importance of setting out the model in such a way that we understand it fully.
Exercise
A possible agricultural project involving small scale woodlots for rapid growth trees has the following flow of net benefits:
Years 0 to 6 Costs of $10 000 a year for fertilizers
Years 7 to 10 Benefits of $60 000 a year from wood
Years 11 to 20 Costs of $20 000 a year because of need to restore land
What is the internal rate of return (i.e. the discount factor which sets the NPV=0) on this project? (The spreadsheet is at ch09ex04.xls.)
This exercise illustrates the folly of using the internal rate of return as a single project evaluative tool. You will find two IRRs for the project, 4.0 percent and 16.1 percent. In general, there are as many IRR's for a project as there are sign changes in the cash flow.
Below is plotted the NPV of this project at various discount rates. The project is justified within the range of IRRs 4 to 16 percent, with maximum net benefits at a discount rate of around 8 percent.
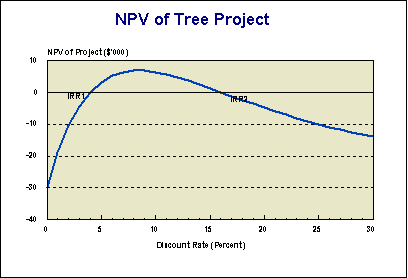 At very low discount rates the
project fails because of the influence of the payments in years 11 to 20 for restoration
of the land. At a discount rate of zero, for example, the project's NPV is simply the
undiscounted sum of the cash flows, - $30 000 ( = (7 * -10 000) + (4 * 60 000) + (10
* -20 000)). Those costs out in years 11 to 20 outweigh the benefits if discount rates are
low enough.
At very low discount rates the
project fails because of the influence of the payments in years 11 to 20 for restoration
of the land. At a discount rate of zero, for example, the project's NPV is simply the
undiscounted sum of the cash flows, - $30 000 ( = (7 * -10 000) + (4 * 60 000) + (10
* -20 000)). Those costs out in years 11 to 20 outweigh the benefits if discount rates are
low enough.
At very high discount rates the project fails because the benefits over years 7 to 10 are discounted too heavily to offset the costs in years 0 to 6, which are discounted less than the benefits. The costs out in years 11 to 20 really don't count at high discount rates - they almost vanish.
At intermediate discount rates the benefits are discounted somewhat, but they are still high enough to overcome the costs in early years, while the long tail costs are discounted enough so that they don't overcome the benefits.
This exercise is a metaphor for projects with a long tail of costs at the end of the project. Decommissioning a nuclear power plant and cleaning up nuclear waste, for example, provides a typical example of such a project.
This exercise also illustrates that it is easy enough to set up the mathematical models, and to get 'correct' solutions. We cannot say we understand discounting, however, until we're confident we can explain what it all means to people who may not have familiarity with the models. We need to be able to tell ministers, foresters and political communities what these figures mean in everyday language.
The exercises on the photocopier and the nursing home are mainly about choosing between mutually exclusive projects. Sometimes the question is whether to undertake a project at all.
In a purely commercial environment decision-makers can use discounted cash flow analysis to decide whether or not to carry out a project at all, looking simply at projected actual cash flows. There is no distinction between economic and financial evaluation. In the public sector we are generally not in a purely commercial situation; we have to take into account benefits and costs which are not associated with cash flows; rather we have to take into account externalities. The exercise below illustrates the distinction between financial and economic evaluation.
Exercise
In the late eighties a private sector consortium considered building a Very Fast Train (VFT). For the preferred inland route their estimates (all in 1988 prices) were:
Construction costs - $5 282 million, spread over two years
Other capital (rolling stock) - $1 188 million in the third year
Operating expenses - $306 million a year, from the third year onwards
Fare - average $123 one way Sydney-Melbourne
Passenger numbers - unknown, but between 6.6 and 8.2 million one way trips annually
The consortium evaluated the project over 16 years (0 to 15), and various discount rate assumptions were tested.
The project is modelled at ch09ex05.xls, for a passenger volume of 8.2 million. Note that this is purely a commercial, or financial evaluation, and that as a commercial project it is not worth doing. But this project would have had a number of external costs and benefits, not shown in this model. Imagine, say, that the project would save $50 million a year road maintenance, and $2.0 billion in year 10 for upgrading roads. This would involve adding $50 million a year to the revenue column, and a further $2 000 million to the revenue column in year 10. If you do that to the base model you will notice the NPV of the project comes to a positive $567 million. This is an example of economic evaluation, which is more comprehensive than financial evaluation. Much of the argument about the VFT, as to whether it is viable or not, is because of a confusion between financial and economic viability.
 Of course this example has
modelled only two hypothetical externalities. Other positive externalities may include
reduction in airport noise, reduction in greenhouse gases, reduction in truck accidents,
and relief on Sydney and Melbourne population pressure if the VFT services a number of
growth centers. Negative externalities may include destruction of animal habitat,
reduction of wilderness values along the route, and loss of land for agricultural or other
purposes (to the extent that this is not reflected in the purchase price).
Of course this example has
modelled only two hypothetical externalities. Other positive externalities may include
reduction in airport noise, reduction in greenhouse gases, reduction in truck accidents,
and relief on Sydney and Melbourne population pressure if the VFT services a number of
growth centers. Negative externalities may include destruction of animal habitat,
reduction of wilderness values along the route, and loss of land for agricultural or other
purposes (to the extent that this is not reflected in the purchase price).
The graph above shows the effect of discounting on this project. The first series is undiscounted; the second series is discounted at 8.0 percent. The suppression of future values is clear from this graph. Even extending it out for a further ten years (which would be quite reasonable for a project of this nature) would not affect the financial viability much. What does make a difference, however, is the choice of discount rate. The last section of this chapter discusses this issue.
Discounting provides a means of taking flows
of costs and benefits over time and converting them to a single lump sum at the beginning
of the period. Annuities present the reverse process; how to convert a lump sum into a
constant flow over a period. Sinking funds are about converting a lumpy set of outlays
into a smooth flow, or accumulating enough money for an expected future outlay.
Annuities
Many people, on retirement, choose (in fact
are strongly persuaded by tax legislation) to convert lump sums into annuities.
If we retire with a lump sum we would like to spin that lump sum out over our remaining
life. We can certainly draw the real interest component, but how fast can we draw down on
the capital component? A benefactor may leave an endowment to a university to fund a chair
for, say, twenty years. How fast can the university draw on the fund? Basically an annuity
is an investment in which we invest a sum S now, or at time 0, and every year,
for n years, draw off a certain amount A. Usually we know S, n,
and r, the rate of return; our task is to find A.
Exercise
Imagine we have accumulated $200 000 in a superannuation policy, and expect to live for twenty years. What can we draw off that policy each year while making sure we leave nothing to the next generation? The discount rate is 5 percent.
We know that if we were to live forever, or if we wanted to leave $200 000 in our will, we could draw off $10 000 a year. We should be able to do better than that however. Now the amount S is simply the present value of a cash flow of A for n years, starting at the end of this year.(3) Then we can simply expand this out as a standard net present value formula:

In the case of a twenty year annuity, substituting n = 20, r = .05, and S = 200 000, we get A = $16 050.We can see from the formula that as n gets very large then the denominator approaches 1. The formula then becomes simply A = Sr, which is the familiar simple interest formula.
If we were not sure we were going to live twenty years, we could, for a management fee, buy a lifelong annuity. These are sold by funds managers, and annual payments are based on statistical life expectancy. If we live for ten years only, bad luck. If we last for thirty years we spend our dotage subsidized by those who went before.
We may find the annuity formula looks a bit formidable. We may find it easier, and more transparent, to use a spreadsheet, and to set up a difference equation model, manipulating the draw off amount A until we have exactly zero after twenty years - a 'suck it and see' approach, which is quite valid mathematically. (Mathematicians use the term iteration, rather than "suck it and see".) For each year we start with an opening capital sum, add the interest, subtract the drawing, and get the residual sum, which becomes the capital for the following year. This is shown in ch09ex06.xls. Using the goal seek function in a spreadsheet we can ask the spreadsheet to do the iterations for us.
Sinking Funds
A sinking fund is a fund to which we make regular payments to meet large expenses in the future. It is a common way of accumulating funds for major building maintenance and refurbishment.
We can develop an accumulation spreadsheet
for a sinking fund for a once-off major outlay (an example is at ch09ex01.xls),
but if our outlays are lumpy and irregular (e.g. paint every five years, re-roof every
thirty years), then our easiest approach is to use a set of difference equations in a
spreadsheet.
Exercise
In the new suburb of Gorton, just south of Yass, the water supply authority has installed new pipes, header tanks, pumps etc.
They estimate the assets will last 30 years before needing replacement. Also, for the first few years, the assets will require virtually no maintenance. They estimate that the following outlays will be required:
They envisage they will have to contribute somewhere between $1 and $2 million a year, and, in order to keep good relations with ratepayers, they want to make sure the contributions start straight away and are the same each year. They can get a real return of five percent for any funds they set aside in a sinking fund.
The spreadsheet is at ch09ex07.xls, and the first fifteen rows of the spreadsheet are shown below. (The spreadsheet shows the full thirty years.) The example below shows a trial contribution of $1.80 million a year, but that is not the right answer; it gives us excess funds of $6.94 million at the end of the period. You will know you have the right contribution rate once the amount left over is zero.
| Sinking fund contribution rate | 1.80 | ||||
| Interest rate | 5% | ||||
| Year | Amt BOY | Interest | Contribution | Drawing | Amt EOY |
| 1 | 0.00 | 0.00 | 1.80 | 0.00 | 1.80 |
| 2 | 1.80 | 0.09 | 1.80 | 0.00 | 3.69 |
| 3 | 3.69 | 0.18 | 1.80 | 0.00 | 5.67 |
| 4 | 5.67 | 0.28 | 1.80 | 0.00 | 7.76 |
| 5 | 7.76 | 0.39 | 1.80 | 0.00 | 9.95 |
| 6 | 9.95 | 0.50 | 1.80 | 0.00 | 12.24 |
| 7 | 12.24 | 0.61 | 1.80 | 0.00 | 14.66 |
| 8 | 14.66 | 0.73 | 1.80 | 0.00 | 17.19 |
| 9 | 17.19 | 0.86 | 1.80 | 0.00 | 19.85 |
| 10 | 19.85 | 0.99 | 1.80 | 2.00 | 20.64 |
| 11 | 20.64 | 1.03 | 1.80 | 2.00 | 21.47 |
| 12 | 21.47 | 1.07 | 1.80 | 2.00 | 22.35 |
| 13 | 22.35 | 1.12 | 1.80 | 2.00 | 23.26 |
| 14 | 23.26 | 1.16 | 1.80 | 2.00 | 24.23 |
| 15 | 24.23 | 1.21 | 1.80 | 2.00 | 25.24 |
A completed spreadsheet does not show the steps
in constructing it. You start with the second last column - the drawings, and incorporate
these into the difference equations - open balance, plus interest, plus regular
contribution, less drawing, equals closing balance. In this case the trial contribution is
$1.8 million a year. You have to experiment with various rates of contribution to get it
right with a zero balance after you have drawn off the $30 million at the end of year 30.(4)
The benefit of a sinking fund for GBEs is
that it allows them to accumulate reserves for projected maintenance and replacement
works; they do not have to raise rates dramatically or go cap-in-hand to the finance
authority when it comes time to make major outlays. It also ensures present users
contribute to expenses they accrue but do not realize. The cost is that, unless it is well
protected, the government can pillage it for current consumption or to close a budget
deficit, especially if the entity is not off-budget. Replacement of ageing infrastructure
is a major problem in many of the world's older cities; in new cities, like Canberra, the
problem is more likely to be that present taxpayers are not paying adequately for future
maintenance, upgrading and replacement.
In most investment decisions the main items of sensitivity are the revenue and the choice of discount rate.
It is customary to use a real, rather than a nominal discount rate in such analysis. In brief, the real discount rate is the nominal rate less inflation.(5) In that way we can do our analysis without having to worry about inflating our cost and revenue elements - all costs and prices can be expressed in constant price terms.
If you are having trouble thinking about real, as opposed to nominal, rates, think back to the exercise in Chapter 1, about a pensioner living off a lump sum. If you had, say, $300 000 to live off, and did not wish to deplete your capital, how much could you draw each year if nominal rates were 12 percent and inflation was 7 percent? The answer is $15 000, or 5 percent of $300 000. Actual interest paid would be $36 000, of course, but inflation has eroded your capital base by 7 percent, or $21 000. You have to put that $21 000 back into the capital base to maintain its real value, leaving you with $15 000 to draw.
Real interest rates (upon which the real discount rate is based) have been volatile in Australia over the eighties, reflecting the use, by successive governments, of monetary policy as a major instrument of economic regulation. Over the long term they average around five percent, but in the short term financial regulators may manipulate rates to influence investment activity. (The effect is mainly on investments with short payback periods, for long-term investors are more interested in long-term interest rates.) Over much of the eighties the western world was gripped by a dogma that government projects were somehow of less value to the community than private enterprise projects; central agencies therefore set very high hurdles for government projects - as high as a ten percent real discount rate - to ration government capital expenditure.
It is questionable whether government authorities should include a premium for risk when choosing a discount rate. In commercial markets lenders always apply a premium for risk. Government securities bear virtually no risk premium; bank bills bear very little. Building society deposits, credit union deposits, unsecured notes, shares, all bear higher risk premiums, depending on the riskiness of the projects in which the institutions lend or invest.
Conventionally, governments used not to apply a risk premium, but now a risk premium is implicit in most discount rates set by central agencies. International credit rating agencies, like Moodys, assess the risk rating of governments, and these flow through to discount rates. Government projects obviously vary in their riskiness - an investment in a road in a congested city is far less risky than an investment as a capital injection to a government owned airline. In general GBEs should use commercial rates, including a premium for risk.
When real interest rates are high, there can be difficulties in choosing an appropriate discount rate. Taking an opportunity cost approach, we should use the opportunity cost of capital - that is, the rate we could get on long term risk free investments - as our benchmark rate. This is sometimes called the social opportunity cost of capital.

On the other hand, many desirable projects would simply not get off the ground at real discount rates as high as 5 or 8 percent. People want to make investments in schooling, environmental protection, or culture, returns from which may not be realized even for generations. In the past communities have embarked on projects which would take hundred of years to complete, such as medieval cathedrals. These decisions, if taken democratically, are governed by a social rate of time preference, which is never zero (our planet may be hit by an asteroid tomorrow), but is often as low as one or two percent, as is revealed by society's choices on education, training etc.
Any notion, therefore, that choice between
competing projects, or the decision whether to undertake a project at all, can be resolved
by recourse to technocratic reductionism, is incorrect. We cannot just take a directive
from headquarters and plug it into our models.
In order to understand not only the mathematics, but also the policy implications of discount rate assumptions, it is useful to run through some questions and exercises:
Discussion questions:
(1) A tree suitable for timber production takes about fifty years to grow; that's an increment of about 2 percent averaged over the period. It is easy to find other investments which yield at least five percent in real terms. Anyone would be a mutt to invest in timber, especially when there's an opportunity to sell twenty year old trees for pulpwood. Why do we still leave trees in the ground for another thirty years?
(2) In commercial activities risk is often associated with competitive factors; the more intense the competition the higher should be the risk premium. Government authorities need not apply such a premium, as they are often in monopoly situations, and, when it comes to the crunch, the government would never let them go broke. Is this correct logic?
Exercise
Until recently, the ACT Electricity and Water Authority offered ratepayers the choice of paying water and sewerage charges in one hit, with a five percent discount, in late September, or spreading the full amount over four equal payments in late September, late November, late January and late March (three payments of $102, and a fourth of $104). If you were a ratepayer in the ACT, which did you choose? If you were not an ACT ratepayer, which would you choose? Set up a model to find the value or penalty in early payment. (As a hint, it's quite valid to use partial years in calculating discount factors. N does not have to be an integer.) The spreadsheet is at ch09ex08.xls.
This exercise is typical of the sort of calculation used in business finance when comparing payment terms for major outlays. Scaled up to several million dollars, timing of payments can make a significant difference.
General References
Most accounting and finance texts have chapters on discounting. One comprehensive reference is Frank S Budnick Applied Mathematics for Business, Economics and the Social Sciences (McGraw Hill 1983)
Specific references and endnotes
1. Some writers use the symbol r, others the symbol i, which strictly equates to the specific entity interest. The term r, short for return, is more general, and can refer to return in the form of interest, dividends or capital gain on loan or equity investment. It can also refer to non-financial returns.
2. It is always arguable whether cash flows should be modelled as occurring at the end of each year, in the middle of each year, or at the beginning of each year. The models are not very sensitive to such variations; if a project does tip as a result of different treatment of cash flow timing within a year it was probably marginal in the first place.
3. This assumes that the last payment of A will come on our dying day - not a great way to organize our finances. We could use it for a funeral and wake. Alternatively we could work on a timing of (n-1).
4. The answer is $1.69547328124984 million, for those who enjoy precision.
5. This represents a minor simplification, in that the nominal rate comprises not only the real rate plus inflation, but also a cross product, being the combined effect of inflation and the real rate. This cross product is usually so small that it can be safely ignored. The inflation assumption is far from unambiguous - it relates to the inflationary expectation over the same period as the discount rate is chosen - thus to get a real discount rate from looking at a ten year Treasury bill, we would have to guess what inflationary expectation is built into that rate.