|
|
The discipline which has come to be known as "human resource management" is often seen as remote from the hard numbers of financial management. But the tools of the demographer and the accountant are highly relevant to personnel planning. What will be the saving resulting from a staffing freeze? (Usually the saving is less than crude estimates suggest.) Can we develop a sensible budget for training, bringing into account all the costs? Will an expansion of our organization put strain on our existing staff?
It is easy to cite examples of poor personnel planning in government. There are recruitment freezes, leading to top-heavy bureaucracies. There are miscalculations of budgets; forecasts based on "common sense" prove to be wildly inaccurate.
Good personnel planning is especially important in the public sector because of the costs of poor planning. These costs are high in the public sector because of:
Staffing models vary from simple back-of-the-envelope calculations ('if our staffing goes up 10 percent our payroll must rise proportionately') through to highly sophisticated models on mainframe computers.
The former are poor, in that they can be inaccurate, and they yield no information about the dynamics of the process of adjustment. The latter are more accurate, but often are accessible only to the high priests of computing, and their internal logic, while often realistic, is too hard for the decision-maker to grasp.
Here our concern is with simple models, based on difference equations, which give some idea of how our systems might behave in response to certain changes in our input variables. What would happen if we instituted a recruitment freeze? What would happen to our salary budget if we expanded 10 percent through base grade recruitment?
The exercises on personnel modelling in this chapter are very simple but powerful in terms of giving some counter-intuitive results. They only touch upon the range of models that can be developed, and are designed to give some inspiration so you can develop your own models. (An excellent text for personnel modelling is Burack and Mathys, which goes into far more complex models.(1)) Spreadsheet models using difference equations are used in epidemiology (e.g. spread of AIDS in Uganda) and in education planning (e.g. demand for school places in Singapore.)
Before the exercises, a few words on equilibrium and stability.
A system is in equilibrium if, in the absence of external disturbance, it stays in the same state from one period to the next. This was seen in the last chapter, in which we saw that the tank would come to an equilibrium.
This is not the same concept as stability. A system is in stable equilibrium if, following a small disturbance, it returns to its equilibrium position; it is in unstable equilibrium if, following a small disturbance, it moves away from that point of equilibrium.
A useful metaphor is a rookie skier, with little control. If the rookie is at the crest of the hill, he or she can stay there indefinitely, but the slightest disturbance will see him or her plummeting to the valley floor. That crest is a position of unstable equilibrium. The valley floor, however, is a position of stable equilibrium - a push, or a chair lift ride, half way up the hill, will see our skier return to the valley floor. (There may be some transient oscillations on the way.)
Unstable Equilibrium - an Example
The town of Numbat has the following population variables:
a birth rate of 2.0 percent a year;
a death rate of 1.5 percent a year;
loss through nett migration of 200 people a year.
We can model this mathematically. The basic difference equation for population P is:
PT+1 = PT + change
= PT + PT * (0.020) - PT * (0.015) - 200
= PT * (1.005) - 200
Now we can set an equilibrium condition, such that PT+1 = PT = PE:
PE = PE * (1.005) - 200
PE = 200/0.005 = 40 000
Thus, we can say Numbat has an equilibrium population of 40 000. But is it stable?
Stokey and Zeckhauser give us a graphical way of modelling
difference equations to test for stability. We can also use spreadsheet simulation.
Exercise
Model Numbat's population on a spreadsheet. Find what happens if its population is varied away from the equilibrium point. Model 40 years of development, and plot its population (beginning of year) against time. (Hint: the key to this, as with any difference equation, is to develop the second line to be copied down. If you are still having trouble, a spreadsheet s at ch06ex01.xls)
Numbat is a metaphor for systems which involve critical mass. There are many examples, the most obvious being country towns in Australia. If they reach a certain size, they may enjoy sustained growth; smaller towns face decline and death. Other examples include voluntary organizations, such as social clubs. Thomas Schelling has developed many critical mass models; for example a social club may not get off the ground unless enough people expect a critical number will turn up to meetings.(2) Sometimes there may be cases for government subsidies to help push systems past this lower equilibrium or critical mass point. Cases for government funded decentralization programs and assistance to voluntary agencies are often framed in terms of critical mass.
The tank system from the previous chapter was an example of a self-correcting system - one which returned to its starting point following a small disturbance. A more comprehensive model of Numbat may reveal at a higher population a different model. Perhaps beyond a population of 200 000, say, it runs up against resource constraints and becomes a less desirable place to live, and migration loss accelerates beyond that point. This upper equilibrium will then become a stable point.
There are many systems with dual equilibria - a critical
mass (unstable) equilibrium at the lower end and a point of diseconomy (stable) at the
upper end.
Let's start with a very simple model.
In our organization we have 2000 staff. We lose 10 percent a year to retirement and resignation. We want to build it up to a larger organization, of 3000, but not too quickly. We know we will have to recruit 300 people a year to maintain a steady number of 3000. If we start recruiting 300 a year now, how long will it take to get up to 3000 staff? On the next page the organization is modelled in a table, generated by a spreadsheet. Note the difference equation form, with the stock at the end of year (EOY) becoming the opening stock at the beginning of year (BOY), one line down. (Because this is a simple model, no spreadsheet is included in the Appendix.)
| Year | Staff BOY A |
Losses (10 % of column A) B | Recruitment C |
Staff EOY (A-B+C) |
| 0 | 2000 | 200 | 300 | 2100 |
| 1 | 2100 | 210 | 300 | 2190 |
| 2 | 2190 | 219 | 300 | 2271 |
| 3 | 2271 | 227 | 300 | 2344 |
| 4 | 2344 | 234 | 300 | 2410 |
| 5 | 2410 | 241 | 300 | 2469 |
| 6 | 2469 | 247 | 300 | 2522 |
The answer, not intuitively obvious, is that we'll never get up to this equilibrium. It
will come close to 3000 staff, but never quite make it - what mathematicians call an asymptotic
function. We can experiment with different approaches, such as recruiting 350 until we
reach 3000:
| Year | Staff BOY | Losses | Recruitment | Staff EOY |
| 0 | 2000 | 200 | 350 | 2150 |
| 1 | 2150 | 215 | 350 | 2285 |
| 2 | 2285 | 229 | 350 | 2407 |
| 3 | 2407 | 241 | 350 | 2516 |
| 4 | 2516 | 252 | 350 | 2614 |
| 5 | 2614 | 261 | 350 | 2703 |
| 6 | 2703 | 270 | 350 | 2783 |
| 7 | 2783 | 278 | 350 | 2854 |
| 8 | 2854 | 285 | 350 | 2919 |
| 9 | 2919 | 292 | 350 | 2977 |
| 10 | 2977 | 298 | 350 | 3029 |
| 11 | 3029 | 303 | 300 | 3026 |
| 12 | 3026 | 303 | 300 | 3024 |
| 13 | 3024 | 302 | 300 | 3021 |
That's better. It involves some overshoot, but we can fine-tune that out of the system. In
any event, at this level of generality these models are not designed to give us specific
targets. They help us answer 'what if' type questions. What if we changed the parameter of
retention, from 90 percent to 95 percent, by way, say, of a retention bonus? The table
below models this effect, with a loss of only 5 percent a year.
| Year | Staff BOY | Losses | Recruitment | Staff EOY |
| 0 | 2000 | 100 | 300 | 2200 |
| 1 | 2200 | 110 | 300 | 2390 |
| 2 | 2390 | 120 | 300 | 2571 |
| 3 | 2571 | 129 | 300 | 2742 |
| 4 | 2742 | 137 | 300 | 2905 |
| 5 | 2905 | 145 | 300 | 3060 |
| 6 | 3060 | 153 | 150 | 3057 |
We get there a lot faster, and may save money in recruiting. (If we keep the retention bonus we'll have to drop our recruiting to 150 once we reach 3000).
We could model an infinite number of variants. The key
point is that such models are built from very simple elements. Each line of the table is
of very simple structure - stock beginning of year, plus flow elements, equals stock end
of year, which becomes the opening stock of the next period. That's the generic model of
difference equations. The elements are simple, but they can model complex and changing
situations. With spreadsheets they are very easy to construct.
Exercise
Develop the above model as a spreadsheet, building in the
capacity to vary your retention rate. (There is no solution provided.)
We can model a more complex situation. Let's consider a public service organization which recruits only through a graduate intake, and starts with the following (stable) staff situation and parameters:
Total staff 180, comprising:
| ASO (Administrative Services Officers) | 120 |
| SO (Senior Officers) | 43 |
| SES (Senior Executive Service) | 17 |
In addition the organization recruits 30 graduates a year, who don't count in the overall establishment.
Every year 80 percent of the graduates are promoted to ASO ranks, 20 percent drop out. Of the ASOs 5 percent each year are promoted to SO, 15 percent retire or move to other organizations. Of the SOs 4 percent each year are promoted to SES, 10 percent retire or move to other organizations. Of the SES 10 percent each year retire or move to other organizations.
The organization has stabilized on this structure, but gets a direction to reduce its size, eventually to reduce to 90 staff. It responds by a recruiting freeze for three years, followed by three years with only 5 recruits, three years with 10, and then taking 15 recruits a year (half its previous intake.) Its total reduction has been 90 recruits (3*15 + 3*10 + 3*5).
This results in an elaborate model (shown below), but the elements are all simple. For each band there is a difference equation structure. The only new elements are promotions 'out' and 'in', which link the bands. Those who are promoted "out" of one band are recruits "in" to the next band in the following period. The number in any band at the end of the year is the number at the beginning of the year, plus promotions "in", less "loss" through retirement, resignation etc.
| Graduates | ASOs | Senior officers | SES | Total | ||||||||||||||
| in | loss | out | boy | in | out | loss | eoy | boy | in | out | loss | eoy | boy | in | loss | eoy | eoy | |
| 0 | 30 | 6 | 24 | 120 | 24 | 6 | 18 | 120 | 43 | 6 | 2 | 4 | 43 | 17 | 2 | 2 | 17 | 180 |
| 1 | 30 | 6 | 24 | 120 | 24 | 6 | 18 | 120 | 43 | 6 | 2 | 4 | 43 | 17 | 2 | 2 | 17 | 180 |
| 2 | 30 | 6 | 24 | 120 | 24 | 6 | 18 | 120 | 43 | 6 | 2 | 4 | 43 | 17 | 2 | 2 | 17 | 180 |
| 3 | 30 | 6 | 24 | 120 | 24 | 6 | 18 | 120 | 43 | 6 | 2 | 4 | 43 | 17 | 2 | 2 | 17 | 180 |
| 4 | 30 | 6 | 24 | 120 | 24 | 6 | 18 | 120 | 43 | 6 | 2 | 4 | 43 | 17 | 2 | 2 | 17 | 180 |
| 5 | 30 | 6 | 24 | 120 | 24 | 6 | 18 | 120 | 43 | 6 | 2 | 4 | 43 | 17 | 2 | 2 | 17 | 180 |
| 6 | 0 | 0 | 0 | 120 | 0 | 6 | 18 | 96 | 43 | 6 | 2 | 4 | 43 | 17 | 2 | 2 | 17 | 156 |
| 7 | 0 | 0 | 0 | 96 | 0 | 5 | 14 | 77 | 43 | 5 | 2 | 4 | 42 | 17 | 2 | 2 | 17 | 136 |
| 8 | 0 | 0 | 0 | 77 | 0 | 4 | 12 | 61 | 42 | 4 | 2 | 4 | 40 | 17 | 2 | 2 | 17 | 118 |
| 9 | 5 | 1 | 4 | 61 | 4 | 3 | 9 | 53 | 40 | 3 | 2 | 4 | 37 | 17 | 2 | 2 | 17 | 107 |
| 10 | 5 | 1 | 4 | 53 | 4 | 3 | 8 | 47 | 37 | 3 | 1 | 4 | 35 | 17 | 1 | 2 | 17 | 98 |
| 11 | 5 | 1 | 4 | 47 | 4 | 2 | 7 | 41 | 35 | 2 | 1 | 3 | 32 | 17 | 1 | 2 | 16 | 90 |
| 12 | 10 | 2 | 8 | 41 | 8 | 2 | 6 | 41 | 32 | 2 | 1 | 3 | 30 | 16 | 1 | 2 | 16 | 87 |
| 13 | 10 | 2 | 8 | 41 | 8 | 2 | 6 | 41 | 30 | 2 | 1 | 3 | 28 | 16 | 1 | 2 | 16 | 84 |
| 14 | 10 | 2 | 8 | 41 | 8 | 2 | 6 | 41 | 28 | 2 | 1 | 3 | 26 | 16 | 1 | 2 | 15 | 82 |
| 15 | 15 | 3 | 12 | 41 | 12 | 2 | 6 | 44 | 26 | 2 | 1 | 3 | 24 | 15 | 1 | 2 | 15 | 83 |
| 16 | 15 | 3 | 12 | 44 | 12 | 2 | 7 | 48 | 24 | 2 | 1 | 2 | 23 | 15 | 1 | 1 | 14 | 85 |
| 17 | 15 | 3 | 12 | 48 | 12 | 2 | 7 | 50 | 23 | 2 | 1 | 2 | 22 | 14 | 1 | 1 | 14 | 86 |
| 18 | 15 | 3 | 12 | 50 | 12 | 3 | 8 | 52 | 22 | 3 | 1 | 2 | 22 | 14 | 1 | 1 | 13 | 87 |
| 19 | 15 | 3 | 12 | 52 | 12 | 3 | 8 | 54 | 22 | 3 | 1 | 2 | 21 | 13 | 1 | 1 | 13 | 88 |
| 20 | 15 | 3 | 12 | 54 | 12 | 3 | 8 | 55 | 21 | 3 | 1 | 2 | 21 | 13 | 1 | 1 | 12 | 88 |
| 21 | 15 | 3 | 12 | 55 | 12 | 3 | 8 | 56 | 21 | 3 | 1 | 2 | 21 | 12 | 1 | 1 | 12 | 89 |
| 22 | 15 | 3 | 12 | 56 | 12 | 3 | 8 | 57 | 21 | 3 | 1 | 2 | 21 | 12 | 1 | 1 | 12 | 89 |
| 23 | 15 | 3 | 12 | 57 | 12 | 3 | 9 | 57 | 21 | 3 | 1 | 2 | 21 | 12 | 1 | 1 | 11 | 89 |
| 24 | 15 | 3 | 12 | 57 | 12 | 3 | 9 | 58 | 21 | 3 | 1 | 2 | 21 | 11 | 1 | 1 | 11 | 89 |
| 25 | 15 | 3 | 12 | 58 | 12 | 3 | 9 | 58 | 21 | 3 | 1 | 2 | 21 | 11 | 1 | 1 | 11 | 90 |
| 26 | 15 | 3 | 12 | 58 | 12 | 3 | 9 | 59 | 21 | 3 | 1 | 2 | 21 | 11 | 1 | 1 | 10 | 90 |
We can see the approach of a recruitment freeze is
effective, but the organization takes some time to stabilize from this shock to the
system. Because the first round is absorbed in the recruiting area it takes some time for
the effect to ripple through the other ranks. ASO ranks reduce almost immediately; SES
ranks do not reduce for seven years. This ripple effect, like a rabbit moving through a
python, is common to many human systems as cohorts move through (e.g. the postwar baby
boomers), or as gaps develop and move through (e.g. the absence of men in postwar USSR).
The ripple effect is shown in the graph below.
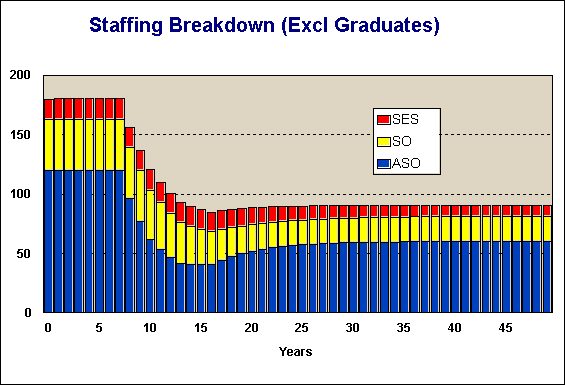
Note the big excess of senior officer level staff a few years after the recruiting freeze.
In fact, while the system comes to total stability fairly quickly, the relativities
between the ranks take a long time to settle down. The next graph shows the 'Indian/Chief'
ratio - the number of ASO plus SO officers for every one SES officer. This drops quickly
as a result of the recruitment freeze, from around 10:1 down to 4:1. That is fairly
obvious without going to the trouble of developing a model; what is less obvious is that
it will take many years to recover to pre-shock levels. Twenty five years after the
initial shock this ratio has still not fully recovered to its previous level. That's a
long time for people to get used to narrower spans of control, to having an excess of
senior officers, and to having few recruits to train.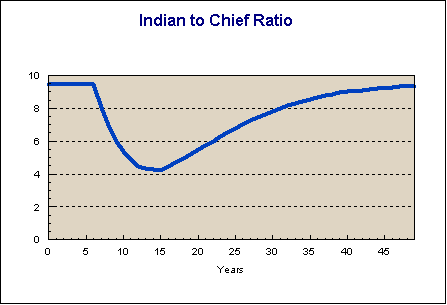
Of course, in anticipation of such a phenomenon, the organization could immediately put a freeze on promotions to the SO or SES level. That would help solve the imbalance problems, but what if promotion has been the only carrot offered by the organization? What if other organizations are offering job opportunities?
There are many other ratios which could be plotted. This model, for example, broadbands the various levels. We may find even greater imbalances at particular levels.
Exercise
Develop the above model, adding in columns for total
payroll and average pay (again ignoring graduates, whose pay comes from a training
allocation). The average pay is: ASO $25 000, SO $45 000, and SES $80 000.
The starting average pay across all staff is $35 000. What is the maximum average pay,
when does it occur, and how long does it take to get back to $35 000? (Spreadsheet ch06ex02.xls)
The previous example illustrated the ripple effect over time. Simple difference equation models can also be used to model a cascade effect through levels of an organization. In an expanding organization, have you ever noticed how so many people seem to be engaged in one of the following activities ('job movement activities'):
This can be modelled, and I have drawn the concepts for the example below from a similar one in Burack and Mathys, making their model a little more general.
The organization presently has 660 staff, and wishes to expand by 10 percent (66 staff) at all levels over the coming year. It has a uniform loss (retirement, moves to other organizations) of 20 percent at all levels.
The present profile is SES 3,4 - 10, SES 1,2 - 20, SOA - 30, SOB - 40, ASO 5,6 - 120, ASO 3,4 - 200, ASO 1,2 - 240. (The terms 'SOA', 'SOB' etc are Australian Government parlance for various levels of middle managers.)
There are seven levels in the organization, and all promotions are internal, except for base grade recruiting.
Each promotion takes around five person-days in terms of people applying for jobs, writing references, panels convening, writing interview reports etc. Once a person has been promoted to a new position he or she will have to go through a learning process, equivalent to four weeks of lost time, before being as productive as the previous incumbent.
Developing the model involves two stages. First we look at gross movements at particular levels. For example, at the SOA level we start with 30 people. We need 3 more (10 percent) to cope with expansion. We will lose 6 (20 percent) through resignation and retirement. Therefore 9 positions need to be filled.
But there is a cascade effect, and to model this we need to start at the top and work down. Starting at the SES 3, 4 level we see we need to take 3 people from the next level down. At that level (SES 1, 2) therefore, we need a total of 9 promotions - 6 because of expansion and loss, 3 because of backfill. And so on down the table. In constructing such a table start at the top and move down, just as you move through time in other difference equation models. Otherwise there are no hard and fast rules.
| Level | Number BOY | Inc | Loss | Total proms | Backfill | Total | |||||
| SES 3, 4 | 10 | 1 | 2 | 3 | 3 | ||||||
| SES 1, 2 | 20 | 2 | 4 | 6 | 3 | 9 | |||||
| SOA | 30 | 3 | 6 | 9 | 3 | 6 | 18 | ||||
| SOB | 40 | 4 | 8 | 12 | 3 | 6 | 9 | 30 | |||
| ASO 5, 6 | 120 | 12 | 24 | 36 | 3 | 6 | 9 | 12 | 66 | ||
| ASO 3, 4 | 200 | 20 | 40 | 60 | 3 | 6 | 9 | 12 | 36 | 126 | |
| ASO 1, 2 | 240 | 24 | 48 | 72 | 3 | 6 | 9 | 12 | 36 | 60 | 198 |
| Total | 660 | 66 | 132 | 198 | 18 | 30 | 36 | 36 | 72 | 60 | 450 |
When we complete the model we find that a ten percent increase in the organization's size is going to involve us in 450 promotions (including 198 recruitments). The completed spreadsheet is at ch06ex03.xls.
If each promotion costs 25 days in output (one week for the promotion process, four weeks in learning the ropes), then promoting (or recruiting) 450 people will cost 11 250 working days (450 * 25), or 56 person years, assuming 200 working days a year.
We can tabulate the effects of various levels of expansion or contraction. We can see that just to stand still (zero percent contraction), the equivalent of 38 persons are devoted to promoting, recruiting, applying for jobs or learning the ropes. For a ten percent expansion this rises to 56 persons, an increase of 18 persons. In other words almost 30 percent of our 66 new workers are devoted to 'job movement activities'. Another way of putting this is that in the first year our ten percent expansion is equivalent to only an effective seven percent expansion of available personnel because of the cost of the job movement activities.
| Percentage increase or decrease | Net expansion or contraction | Number of promotions | Equivalent days | Equivalent staff |
| -20 | -132 | 0 | 0 | 0 |
| -10 | -66 | 150 | 3 750 | 19 |
| 0 | 0 | 300 | 7 500 | 38 |
| 10 | 66 | 450 | 11 250 | 56 |
| 20 | 132 | 600 | 15 000 | 75 |
| 30 | 198 | 750 | 18 750 | 94 |
It is also notable that a twenty percent contraction in this organization results in no job movement activity at all. That's the equivalent of 38 full time staff liberated from such activities. This is one reason why a contraction may be easier to absorb in the short term than in the long term. (Of course there are other countervailing short term costs of reducing size.)
This exercise is at ch06ex03.xls.
The main point is that we can model staffing dynamics, and
such models, while being built from simple elements, are powerful tools in helping us
understand and plan.
Markov models are particular models for handling processes in closed systems, where the total population doesn't change over time. Texts on Markov models, such as Stokey and Zeckhauser, talk about the transition matrix describing the movements between two points of time, and suggest using matrix algebra to model Markov processes.(3)
It is also practical to model simple Markov processes as difference equations.
A simple Markov process is to model changes in the labour market in a closed community. Disappointment Springs has a labor force of 10 000, who are either employed or unemployed. Of those employed in any one year 95 percent stay employed in the following year. Of those unemployed in any one year 65 percent stay unemployed in the following year.
Our first step is to write the transition matrix as a table, making sure the rows add to 1. (That is, there will be no losses out of the system.)
| Next period | ||||
| Employed | Unemployed | Total | ||
| This period | Employed | 0.95 | 0.05 | 1.00 |
| Unemployed | 0.35 | 0.65 | 1.00 | |
The elements in the matrix describe one's chances of
moving from one state to another, or of staying in the same state. I can come to be
employed next period in one of two ways - having been employed last period (a 95 percent
chance of keeping my job) or having been unemployed (a 35 percent chance of getting a
job). Similarly for being unemployed.
Exercise
Develop this exercise as a spreadsheet difference equation model, starting with employment of 7000. An extract from the spreadsheet is shown below. Will it stabilize; if so, at what level? The spreadsheet, without formulae, is shown below, and the full spreadsheet can be accessed at ch06ex04.xls.
| Markov Model - Disappointment Springs Labor Force | ||||
| Next Period | ||||
| Employed | Unemployed | Total | ||
| This period |
Employed | 0.95 | 0.05 | 1.00 |
| Unemployed | 0.35 | 0.65 | 1.00 | |
| Period | Employed | Unemployed | Total | |
| 0 | 7 000 | 3 000 | 10 000 | |
| 1 | 7 700 | 2 300 | 10 000 | |
| 2 | 8 120 | 1 880 | 10 000 | |
| 3 | 8 372 | 1 628 | 10 000 | |
| 4 | 8 523 | 1 477 | 10 000 | |
| 5 | 8 614 | 1 386 | 10 000 | |
Such labor force models are more than teaching abstractions. The ABS, for example, publishes labor force transition data, which is replicated below for the Australian labor force between July and August 1993.
| Transition Matrix for Australian Labor Force - July - August 1993 | ||||||
| Labor force status August 1993 | ||||||
| Employed FT | Employed PT | Unemployed | Not in labor force | Total | ||
Labor force status July 1993 |
Employed FT | 0.941 | 0.034 | 0.010 | 0.015 | 1.000 |
| Employed PT | 0.098 | 0.786 | 0.032 | 0.084 | 1.000 | |
| Unemployed | 0.061 | 0.076 | 0.697 | 0.166 | 1.000 | |
| Not in labor force | 0.011 | 0.026 | 0.033 | 0.930 | 1.000 | |
| Source: Derived from Table 34 of ABS Cat 6203.0 The labor Force August 1993 | ||||||
Exercise
In a certain country there have been two airlines - Ozair and Abelair. They have shared the market (now around 1 million passengers a month) since Lawrence Hargrave took to the air in 1894. They have had 50 percent of the market each.
This month there is a new entrant - Compair. Market research has shown that to date most consumers are not particularly loyal to specific airlines, but they are generally loyal to the two airline system. If dissatisfied with Ozair, which most of them are, most switch their next patronage to Abelair. Likewise for Abelair.
Only a few will drop out to try Compair, but once they do they're very satisfied, with only a small number coming back to the older airlines.
Market researchers have confirmed this in producing the following transition matrix:
| This month | Next month | ||
| Ozair | Abelair | Compair | |
| Ozair | 0.25 | 0.72 | 0.03 |
| Abelair | 0.72 | 0.25 | 0.03 |
| Compair | 0.10 | 0.10 | 0.80 |
We can construct this as a spreadsheet model, with different starting conditions. See ch06ex05.xls. Some 'pure' models you can simulate are:
1. Loyalty:
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
This is a trivial case - it simply locks in the starting conditions. It is not really a 'transition' matrix as there is no transition.
2. Indifference:
| .333 | .333 | .333 |
| .333 | .333 | .333 |
| .333 | .333 | .333 |
This immediately dissipates the starting condition, stabilizing at predictable shares.
3. Rejection:
| 0.0 | 0.5 | 0.5 |
| 0.5 | 0.0 | 0.5 |
| 0.5 | 0.5 | 0.0 |
Individuals exhibit cyclical behavior, but the aggregate will not necessarily be cyclical. (For most starting conditions this system oscillates a little before stabilizing.)
4. Trial and error to new loyalty:
| 0.0 | 0.5 | 0.5 |
| 0.5 | 0.0 | 0.5 |
| 0.0 | 0.0 | 1.0 |
This is an absorbing matrix, in that the system slowly moves to a new stable state. Depending on starting conditions there may be some oscillation. Absorbing matrices are sometimes observed in epidemiology, with a disease slowly being eradicated.
5. Ring a rosy (moving in a set sequence):
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
The behavior of the system is highly dependent on starting conditions. Under most starting conditions it is cyclical. While the model generates pretty patterns, it's hard to imagine applicability to real situations.
Specific References
1. Elmer H Burack and Nicholas J Mathys "Basic Forecasting Models and Methods" Ch 6 in Human Resource Planning - A Pragmatic Approach to Manpower Staffing and Development (Brace Park Press Il 1987)
2. Thomas C Schelling Micromotives and Macrobehavior (W W Norton 1978).
3. Edith Stokey & Richard Zeckhauser A Primer for Policy Analysis (W W Norton NY 1978)