|
|
Much financial data that comes to us, from internal or external sources, is in the form of time series - average weekly earnings, expenditure on roads, taxation revenue. Often, such as when we are preparing forward estimates, we want to get some idea of historical trends so we can project future years' expenditure, revenue or other financial flows.
Unfortunately financial data usually contains the 'noise' of inflation. Simply looking at a column of figures, it's very hard to judge, quickly, what has been the effect of inflation, or general increases in prices, and therefore it's very hard to judge what have been the underlying trends.
Imagine, for example, that we wanted to see how much Australians had been paying in wholesale sales tax (WST) and fuel excise over recent years before the introduction of the GST.
The first thing we would have to do is to bring that data to a per capita series. Population has been growing, so it is natural that taxes will have been growing. This data is shown in the table below.
| Components of Federal Consumption Taxes | ||||||
| Year | WST $m | Fuel excise $m | Popn '000 | WST $ /head | Fuel excise $ /head | Total $ /head |
| 80-81 | 2 102 | 925 | 14 923 | 141 | 62 | 203 |
| 81-82 | 2 854 | 970 | 15 184 | 188 | 64 | 252 |
| 82-83 | 3 490 | 1 364 | 15 394 | 227 | 89 | 315 |
| 83-84 | 4 165 | 2 137 | 15 579 | 267 | 137 | 405 |
| 84-85 | 4 966 | 2 387 | 15 788 | 315 | 151 | 466 |
| 85-86 | 5 728 | 3 087 | 16 018 | 358 | 193 | 550 |
| 86-87 | 6 348 | 5 217 | 16 264 | 390 | 321 | 711 |
| 87-88 | 7 547 | 5 426 | 16 532 | 457 | 328 | 785 |
| 88-89 | 9 402 | 5 828 | 16 814 | 559 | 347 | 906 |
| 89-90 | 10 132 | 6 416 | 17 065 | 594 | 376 | 970 |
| 90-91 | 9 365 | 6 642 | 17 284 | 542 | 384 | 926 |
| 91-92 | 9 113 | 7 093 | 17 494 | 521 | 405 | 926 |
| 92-93 | 9 252 | 7 200 | 17 677 | 523 | 407 | 931 |
| 93-94 | 10 414 | 8 499 | 17 854 | 583 | 476 | 1 059 |
| 94-95 | 11 624 | 9 406 | 18 072 | 643 | 520 | 1 164 |
| 95-96 | 12 955 | 10 224 | 18 311 | 707 | 558 | 1 266 |
| 96-97 | 13 308 | 10 543 | 18 532 | 718 | 569 | 1 287 |
| 97-98 | 14 085 | 10 895 | 18 751 | 751 | 581 | 1 332 |
| 98-99 | 15 080 | 9 521 | 18 973 | 795 | 502 | 1 297 |
| 99-00 | 15 450 | 9 635 | 19 917 | 776 | 484 | 1 259 |
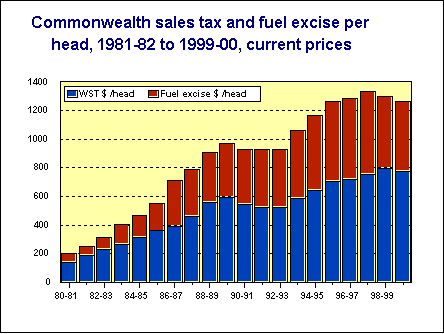 As
we'd expect, tax payments have gone up, and quite steeply, but so too has everything else
over the period - wages, prices etc. If we look at the graph over the page, there is
little we can tell; the noise of inflation is just too much. For someone to tell us the
value of something in 1980-81 currency, and then to ask us to compare that with something
in 2000-01 currency, is like asking us to compare two amounts, one in Roubles and the
other in Yen. We need some way to bring these to a common measure. To continue with the
currency metaphor, we need a set of "exchange rates" to bring these to a
consistent series. Such "exchange rates" can be built up by use of price index
numbers.
As
we'd expect, tax payments have gone up, and quite steeply, but so too has everything else
over the period - wages, prices etc. If we look at the graph over the page, there is
little we can tell; the noise of inflation is just too much. For someone to tell us the
value of something in 1980-81 currency, and then to ask us to compare that with something
in 2000-01 currency, is like asking us to compare two amounts, one in Roubles and the
other in Yen. We need some way to bring these to a common measure. To continue with the
currency metaphor, we need a set of "exchange rates" to bring these to a
consistent series. Such "exchange rates" can be built up by use of price index
numbers.
The graph doesn't really tell us much; is all we are seeing is the result of lower inflation in the nineties, or is something more happening? What we need is a constant price series so that all this data is to a common price base, but first, a word on index numbers.
Price index numbers are developed by comparing the price of a basket of goods and services in a base year with the price of the same basket of goods and services in the current year. (That's just like looking at the prices, in local currencies, of a bundle of goods and services in Japan and a similar bundle in Russia, and using those prices to infer a Yen/Rouble exchange rate.) The price in the base year is normalized by bringing it to 100. The basket (also technically called a regimen) for a consumer price index is the set of goods and services consumed by an average household. Another way of looking at a series of price index numbers is to say that if the index number in the base year is 100, and in a later year is 100 + X, then the purchasing power of $100 + X in the later year is the same as the purchasing power of $100 in the base year.
This is the definition of the standard Laspeyres index numbers. There are others, but they are not in common use.
Mathematically:
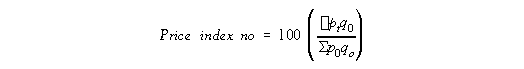
Where p0 and pt are the prices in the base period and the period t, and q0 are the quantities in the base period. Basically the term Sigma ptq0 is the amount our consumer would have to spend, in period t, to buy the same basket of goods and services as he or she bought in period 0.
Although the formulae show q0 as unchanging, the baskets do change through a process called splicing. (A case in Australia involved finding a substitute for seamed silk stockings which had appeared in the old basic cost of living index.) A new series is developed with a new basket, and the old series is spliced on to it by simple mathematical proportions.
This bit of mathematics may look daunting, but it is conceptually simple, as demonstrated by working through an example, looking at the prices of an identical bundle over two successive years..
Exercise
Life is tough for students. In a fit of generosity the Commonwealth has decided to index Austudy student assistance to living costs. This cost of living index is not the Consumer Price Index; rather it is based on a special basket of goods and services used by students.
Through extensive and painful research statisticians have surveyed the average
expenditure of undergraduates, and have established that there are only 17 items on which
these poor wretches spend their money. They have found how much of each item the average
student buys. By surveying the cafeteria, dorms, Salvation Army clothing depots etc, they
have also been able to find what the prices of these 17 items were in January 2000 and in
January 2001. The task is to construct an index number from their data.
| Undergraduate Student's Cost of Living | ||||||
| Item | Unit | Weekly consumption Jan 00 | Unit price Jan 00 | Weekly expenditure Jan 00 | Unit price Jan 01 | Weekly exp Jan 01 |
| Jeans | pair | 0.020 | 35.00 | 36.00 | ||
| T shirt | 0.050 | 12.00 | 13.00 | |||
| Sneakers | pair | 0.030 | 40.00 | 42.00 | ||
| Underpants | pair | 0.040 | 5.00 | 4.00 | ||
| Brassiere | 0.020 | 7.00 | 6.00 | |||
| Sock | pair | 0.020 | 3.00 | 3.00 | ||
| Sweater | 0.020 | 40.00 | 42.00 | |||
| Meat pie | 7.000 | 1.20 | 1.80 | |||
| Hot dog | 7.000 | 1.40 | 1.50 | |||
| Beer | 750 ml | 7.000 | 1.80 | 2.50 | ||
| Wine | 4l cask | 1.000 | 8.00 | 8.00 | ||
| Car parts | basket | 0.006 | 180.00 | 190.00 | ||
| Car deprec | 12 yr VW | 0.002 | 3000.00 | 3100.00 | ||
| Gasoline | liter | 15.000 | 0.67 | 0.75 | ||
| Bus fare | section | 2.000 | 0.70 | 0.75 | ||
| Books | basket | 0.040 | 42.00 | 43.00 | ||
| Rent | dorm wk | 1.000 | 50.00 | 52.00 | ||
| Cost of living | ||||||
| Index number | ||||||
The spreadsheet is at ch07ex01.xls If you get it right you
will find the answer, for the index number in January 2001, base January 2000, is 112.0.
But is this a fair calculation; what limitations are there in the methodology, which is
the standard methodology in constructing index numbers? The main limitation is known as
the substitution effect, which means that when prices are rising
non-uniformly, price index numbers tend to overstate rises in the cost of living. After
all, they measure what it would cost to buy the same basket of goods and services, but if
some items have risen in price faster than others, would not the average consumer
substitute some of the items which have risen in price more slowly? (For an example, look
at beer and wine in the table above.)
We can go back to our original problem, and can use the consumer price index to update it. The general rule for bringing a value expressed in current prices to a constant price series is:

The base year for the series can be the same as the base year of the index number, or any other base year.
 For
example, Australians spent $3 177 million in electrical goods stores in 1982-83. What is
this in 1999-00 prices?
For
example, Australians spent $3 177 million in electrical goods stores in 1982-83. What is
this in 1999-00 prices?
From the ABS Consumer Price Index, we see that the CPI in 1982-83, base 1989-90, was 60.8. In 1999-00, base 1989-90, it was 124.7.
Even before we do a formal calculation we can see the CPI has roughly doubled. Therefore our answer should be around $6.4 billion.
More precisely, the value, in 1990-00 prices, was 3 177 * 124.7 / 60.8 = $6 516 million. Note that although the ABS publishes an index number base 1989-90, we are using a base of 1999-00 for our constant price estimate. We can use any base year we wish; in general it's easiest to think of prices in the units most familiar to us - that is, the present year or the most recent one for which an index number is available.
It's a good idea to check our calculations against common sense. Bringing a series to constant prices should tend to flatten it out; if the changes become more marked we have probably made an error somewhere along the line.
We can come back to the series at the start of this chapter, and update it using the ABS CPI data. See the exercise ch07ex02.xls We have departed a little from standard textbook presentation, by adding the column "exchange rate".
Components of Federal Consumption Taxes |
||||||||
Current Prices |
Constant (93-94) Prices |
|||||||
| WST/ head | Fuel excise/ head | Total/ head | CPI base 89-90 =100 | "Exchange rate" | WST/ head | Fuel/ head | Total/ head | |
| 80-81 | 141 | 62 | 203 | 49.5 | 2.52 | 355 | 156 | 511 |
| 81-82 | 188 | 64 | 252 | 54.6 | 2.28 | 429 | 146 | 575 |
| 82-83 | 227 | 89 | 315 | 60.8 | 2.05 | 465 | 182 | 647 |
| 83-84 | 267 | 137 | 405 | 65.0 | 1.92 | 513 | 263 | 776 |
| 84-85 | 315 | 151 | 466 | 67.8 | 1.84 | 579 | 278 | 857 |
| 85-86 | 358 | 193 | 550 | 73.5 | 1.70 | 607 | 327 | 934 |
| 86-87 | 390 | 321 | 711 | 80.4 | 1.55 | 605 | 498 | 1103 |
| 87-88 | 457 | 328 | 785 | 86.3 | 1.44 | 660 | 474 | 1134 |
| 88-89 | 559 | 347 | 906 | 92.6 | 1.35 | 753 | 467 | 1220 |
| 89-90 | 594 | 376 | 970 | 100.0 | 1.25 | 740 | 469 | 1209 |
| 90-91 | 542 | 384 | 926 | 105.3 | 1.18 | 642 | 455 | 1097 |
| 91-92 | 521 | 405 | 926 | 107.3 | 1.16 | 605 | 471 | 1077 |
| 92-93 | 523 | 407 | 931 | 108.4 | 1.15 | 602 | 469 | 1071 |
| 93-94 | 583 | 476 | 1 059 | 110.4 | 1.13 | 659 | 538 | 1197 |
| 94-95 | 643 | 520 | 1 164 | 113.9 | 1.09 | 704 | 570 | 1274 |
| 95-96 | 707 | 558 | 1 266 | 118.7 | 1.05 | 743 | 587 | 1330 |
| 96-97 | 718 | 569 | 1 287 | 120.3 | 1.04 | 744 | 590 | 1334 |
| 97-98 | 751 | 581 | 1 332 | 121.0 | 1.03 | 774 | 599 | 1373 |
| 98-99 | 795 | 502 | 1 297 | 121.8 | 1.02 | 814 | 514 | 1328 |
| 99-00 | 776 | 484 | 1 259 | 124.7 | 1.00 | 776 | 484 | 1259 |
To see how this works, we can look at a typical cell - the figure for WST/head in 1980-81
expressed in 1999-00 prices. It is 141 * 124.7 / 49.5 = 355. The figure for fuel
excise/head in 1988-89 expressed in 1999-00 prices is 347 * 124.7/92.6 = 467. Note that in
a spreadsheet you would freeze the reference to the CPI of 124.7 in 1999-00, or perhaps
name it.
Note that in the final year, 2000-01, the current year value and the constant price series converge. That is another check on your calculations.
 You
may find the term current prices a little confusing; the word
'current' doesn't mean 'today'; rather it means prices which were current when the
observation was made.
You
may find the term current prices a little confusing; the word
'current' doesn't mean 'today'; rather it means prices which were current when the
observation was made.
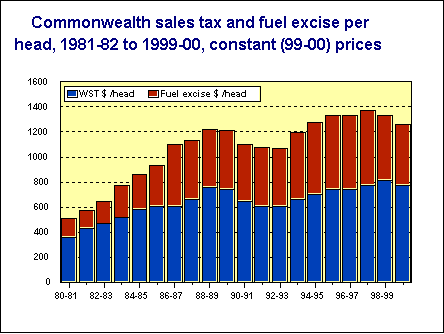
The result of this manipulation is shown in the graph alongside. Note that the noise has gone out of it, and it is much less steep, but still rising up to 1989-90. The decline and subsequent recovery becomes evident once we have normalized the series for population growth and for inflation; compare this with the original series at the start of this chapter which suggested steady growth in taxation revenue. As a general rule taxes of all sorts decline during a recession.
This presentation shows some of the reason for the introduction of the GST. Wholesale sales tax collection had levelled off. Many of the goods subject to high rates of tax have become cheaper, as a result of technological developments and lowering tariffs, and, in general, consumption of goods is rising less quickly than consumption of services. Note too that fuel excise collections have been more steady since the mid eighties, when excise rates were indexed to the CPI (subsequently abandoned in a political panic in early 1991). What the graph reflects, therefore, is mainly changes in physical consumption.
Exercise
Below are the prices for a long distance daytime call from Sydney to Perth. What has happened in real (inflation adjusted) terms?
| Price of Three Minute Telephone Call - Sydney/Perth - Day Rate | |||
| Current Prices | CPI Base 1989-90 = 100 | Constant Prices | |
| 1960 | £0/15/0 | 14.1 | |
| 1965 | £0/15/0 | 15.3 | |
| 1970 | $1.80 | 18.0 | |
| 1975 | $2.16 | 30.4 | |
| 1980 | $2.70 | 49.5 | |
| 1985 | $1.92 | 73.5 | |
| 1990 | $1.72 | 105.3 | |
| 1995 | $1.62 | 111.9 | |
| 2000 | $0.71 | 124.7 | |
The spreadsheet is at ch07ex03.xls. In this case the constant
price series has more variation than the current price series, which is an exception to
the general rule.
Exercise
Below are some prices of consumer goods in 1960. (All prices are taken from pre-Christmas advertisements in the Sydney Morning Herald). Express these prices in 1999-00 prices. (The CPI figures are 14.1 for 1960, as in the previous exercise, and 124.7 for 1999-00.) Another perspective is that in 1960 the minimum adult male weekly wage was £18 (females £12), and the average male wage was £23. By 2001 the average male ordinary time wage was around $840.
(For those who have not had to labor under the British price system, a Pound subdivided into 20 shillings, which subdivided into 12 pence, which divided into halfpennies and farthings (a quarter penny). A Guinea was 21 shillings; it was designed by lawyers to give themselves a 5 percent tip on every transaction. In 1966 £1/0/0 became $2.00.)
| Mercedes 220 SE | £3 100 |
| Holden station wagon | £1 290 |
| Vauxhall Velox | £1 463 |
| Ford Anglia | £974 |
| Balmain 2 bed brick cottage | £2 850 |
| Granville 3 bed, 5 mins from station | £3 900 |
| Elizabeth Bay, 2 bed unit, harbor and park views, private jetty | £8 600 |
| Mosman, 3 bed plus study, harbor views | £14 975 |
| Men's woollen sport coat (Hordens) | £12/19/6 |
| Brassiere, cotton, basic (Hordens) | 27/6 |
| Men's nylon socks (Hordens) | 3/11 |
| Manual calculator | £45/0/0 |
| Astor auto washer | 199 Gns |
| Victa 'Four Star' mower | 62 Gns |
| Waltham gent's watch (no date) | £18/15/0 |
| Hoover steam and dry iron | £10/10/0 |
| HMV transistor portable radio | 29 Gns |
| AEI Ekco 23" TV | 209 Gns |
| Kodak 'Retinette' camera | £22/10/0 |
| Kodak basic 127 B&W camera | £1/15/9 |
| Astor medium sized refrigerator | 179 Gns |
| Set of six wine glasses | £1/3/6 |
| 'Queen Anne' Mahogany china cabinet | £83/14/0 |
| Tripod polished wooden wine table | 99/6 |
(There is no solution sheet with this exercise.)
This concludes the mathematics of price index numbers. In a country with a tradition of central wage fixing, and measures such as indexation of pensions, measurement of the CPI is a very important issue. In setting a CPI should one-off discounted prices be used? Should changes in quality be taken into account? How are new index numbers spliced? How is the 'average' household measured to get a basket in the first place? How should rent, insurance etc be treated?
Sometimes special groups argue for special index numbers. The ageing, for example, may argue that since health care prices are rising much faster than prices generally, they should have a special basket for pension indexation, as health care is so important in their consumption.
This chapter has been concerned with the consumer price index. There are many other indexes - import price index, GDP deflator (a deflator is similar to an index number, but usually is normalized to 1 rather than 100, and is expressed as a reciprocal(1)), price index of materials used in building etc. They all involve the same basic construction, are used in similar ways, and have the same limitations.
General References
P H Karmel "Price Index Numbers" Chapter 12 in Applied Statistics for Economists (Pitman 1965)
R Lipsey, P Steiner, D Purvis "Index Numbers" Chapter 3 in Economics (Harper and Row 1984)
Australian Bureau of Statistics Consumer Price Index Cat 6401.0 - various editions.
Australian Bureau of Statistics - Surviving Statistics (ABS 1992)
Budget Statements - Budget Paper #1 - various editions
Specific References
1. For example, if the CPI were expressed as a deflator base 1989-90 = 1.000, then the deflator for 1991-92 would be 100.0/107.3, or 0.932.