|
|
Return to toc
The term life cycle costing, also called all-of-life-costing, refers to a means to integrate evaluation of purchase, operating, and disposal costs of assets.
The notion that we should think about costs in such an integrated way is, perhaps, no more than commonsense. Domestically, when we buy an electrical appliance, prudence dictates that we should look at its durability and energy consumption. In government, however, poorly developed accounting systems, budgetary systems with incentives to consider only short term cash outlays, and separation of responsibility for purchasing and using assets, can make for unwise purchasing.
Poor accounting systems, for example, will not pick up all the costs of purchasing; thus a trip to evaluate a foreign supplier may be debited against "travel", rather than against the purchase concerned. (Such poor accounting may often discriminate against local suppliers.)
Shortcomings such as this can be overcome with self-evident accounting, organizational and budgetary reform. Devolution of purchasing and operating responsibility to the one area is a sensible approach.
But analytically it is not always easy to choose between competing alternatives. In Chapter 9 we saw how to use discounted cash flow analysis to choose between projects with different mixes of purchase and operating costs. The trade off is generally between assets with high purchase/low running costs, and those with low purchase/high running costs.
In those exercises we restricted our examples to situations where the assets had identical lives. That made the decision rule simple; choose the alternative with the lowest NPV of costs. (Or, in the case of assets with outputs which can be valued, the highest NPV of benefits or lowest NPV of costs.)
In practice, however, assets do not have identical lives. Often we have to choose between expensive but long life assets, and lower purchase price but shorter life assets. Also we often have to decide on an appropriate time to dispose of assets, for as an asset ages maintenance costs inevitably rise. Simply taking the NPVs in such cases is not a reasonable basis for comparison.
This chapter considers, by illustration, two approaches. The conventional approach is to take the present values of the competing proposals, and, using an annuity formula, to convert these to regular periodic outlays, so we can make comparisons on the basis of annualised costs. An easier approach is to short circuit the process and, using a difference equation model, to find the equivalent periodic outlays.
Imagine a typical private decision - whether or not to trade in an old car on a new one. The old car is losing trade-in value and is starting to cost more in maintenance. On the other hand there would be a big cash outlay to buy a new car. If we have the cash there is an opportunity cost in terms of interest foregone; if we do not have the cash we would need to borrow the money and pay interest.
The way to look at the problem is to disregard normal variable operating costs (routine service, gasoline, tires), and normal time related costs (registration, compulsory insurance), as these would be incurred regardless of whether or not we had a new or old car. The relevant items to include in any analysis are:
We can start at any point in time, but, mathematically, it's easiest to look at one life cycle, starting at the beginning. Therefore, we can re-frame the problem. We are about to buy a new car, and we want to keep it for n years. What is the value of n which gives us most economical service over this period?
The conventional technique, as outlined in accounting texts, is to look at all our options (different values of n), and to go through a two step process:
Step 1.Bring all outlays and receipts to net present value, using discounting.
Step 2.Convert these NPVs to a time based flow, converting the NPVs into annuities.
Step 1 would be sufficient for comparing projects with a similar service life times.
If, for example, we were looking at two different cars, both of which we would keep for
ten years, but with different purchase and running costs, then Step 1 would suffice. We
would simply choose the option with the lowest NPV. In general, however, we cannot use NPV
analysis alone to solve such problems. (An exception comes when our service lives are
simple whole number multiples of one another. For example we can compare one cycle of a
ten year asset with two cycles of a five year asset.)
Example - Life Cycle Costing of Cars
Imagine you are considering how long to keep a car which costs $25 000 new. The trade-in value after three years would be $15 000, after six years $10 000, after nine years $5 000, and after twelve years zero. Over the first three years there would be no extra maintenance, over the next three years there would be $500 extra maintenance required each year, over the following three years an extra $1 000 maintenance, and over the following three years an extra $2 000 maintenance a year. These figures are summarized in the table below. (Note that we are considering the first year as year 0, therefore the final year as year 11.)
| Year | Purchase | Trade in value | Extra mtce |
| 0 | -25 000 | ||
| 1 | |||
| 2 | 15 000 | ||
| 3 | -500 | ||
| 4 | -500 | ||
| 5 | 10 000 | -500 | |
| 6 | -1 000 | ||
| 7 | -1 000 | ||
| 8 | 5 000 | -1 000 | |
| 9 | -2 000 | ||
| 10 | -2 000 | ||
| 11 | 0 | -2 000 |
It is reasonably easy to construct a series of NPV tables. These are shown below, for a
discount rate of 10 percent (a typical real rate faced in domestic purchasing).
| Keep 3 Years | Keep 6 years | Keep 9 years | Keep 12 years | ||||||
| Year | Disc factor | Cash outlays & receipts | Cash outlays & receipts | Cash outlays & receipts | Cash outlays & receipts | ||||
| Original | Discounted | Original | Discounted | Original | Discounted | Original | Discounted | ||
| 0 | 1.0000 | -25 000 | -25 000 | -25 000 | -25 000 | -25 000 | -25 000 | -25 000 | -25 000 |
| 1 | 0.9091 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0.8264 | 15 000 | 12 397 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0.7513 | -500 | -376 | -500 | -376 | -500 | -376 | ||
| 4 | 0.6830 | -500 | -342 | -500 | -342 | -500 | -342 | ||
| 5 | 0.6209 | 9 500 | 5 899 | -500 | -310 | -500 | -310 | ||
| 6 | 0.5645 | -1 000 | -564 | -1 000 | -564 | ||||
| 7 | 0.5132 | -1 000 | -513 | -1 000 | -513 | ||||
| 8 | 0.4665 | 4 000 | 1 866 | -1 000 | -467 | ||||
| 9 | 0.4241 | -2 000 | -848 | ||||||
| 10 | 0.3855 | -2 000 | -771 | ||||||
| 11 | 0.3505 | -2 000 | -701 | ||||||
| NPV | -12 603 | -19 818 | -25 239 | -29 892 | |||||
This, in itself, does not guide us very far in our choice, because each is for a different
time period. We know that to trade in after three years (at the end of year 2) the cash
flow is equivalent to outlaying $12 603 now, to trade in after six years the cash
flow is equivalent to outlaying $19 818 now, and so on.
To give comparative data we need to bring these back to regular periodic outlays. The task is to find what regular periodic outlay A over n years (where n in this case has the value 3, 6, 9 or 12) has the present value S, where S is one of the present values calculated above, and the discount rate is r . This is given by the annuity formula, shown below.
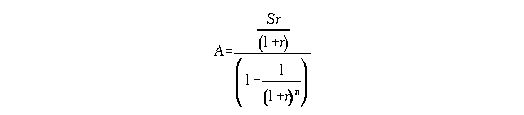
(This formula is slightly different from that shown in Chapter 9, for in this case our starting year is year 0; in the formula in Chapter 9 the starting year is assumed to be year 1. This distinction is to bring the formula into line with the convention in DCF analysis, calling the first year 0.)
It's a daunting piece of work, but can be calculated from first principles. For those interested in the derivation of this equation, this is given below:
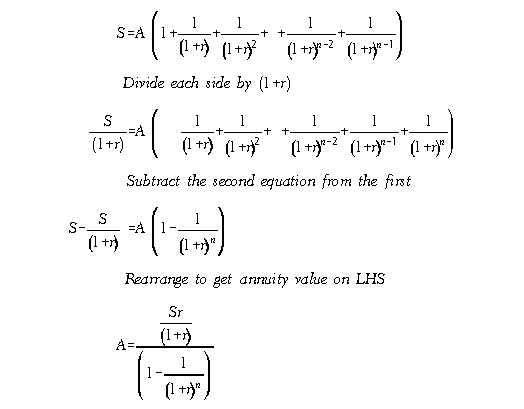
Substituting these formulae, we get the period annuity payments to be:
The decision, then, would be to go for a nine year turnaround. The spreadsheet is at ch13ex01.xls.
There is, fortunately, a simpler path to this result. A little less mathematically virtuous, perhaps, but certainly just as valid.
We can start with the question "What regular annual payment would be required to finance this cash flow?". This is the same as the sinking fund problem in Chapter 9 To illustrate, take one of the cases, the nine year option.
In a spreadsheet start with the years in the left column and outlays ("drawings") in the fifth column. The other columns will be used to set up a set of difference equations. You should also leave a few rows at the top.
Year |
Amount BOY | Interest | Contribution | Drawing | Amount EOY |
| 0 | -25 000 | ||||
| 1 | 0 | ||||
| 2 | 0 | ||||
| 3 | -500 | ||||
| 4 | -500 | ||||
| 5 | -500 | ||||
| 6 | -1 000 | ||||
| 7 | -1 000 | ||||
| 8 | 4 000 |
We need to set up a regular contribution which will set the residual amount left at the
end of year 8 to zero. The opening amount of our fund will be zero. The difference
equation format will be:
Amount end of year
= Amount beginning of year
+ Interest
+ Contribution
+ Drawing (expressed as negative)
The figure contribution is, of course, our unknown. Here's where we can use the mathematical construction "suck it and see", more rigorously called iteration, or Goal Seek in Excel. (These processes are described in Chapter 9.) We set up a table with a trial contribution, and vary it till the residual is zero. The table below shows the completed calculation, and you will note the result, $3 984, is the same as that achieved with the other method.
| Trial contribution | 3 984 | ||||
| Year | Amount BOY | Interest | Contribution | Drawing | Amount EOY |
| 0 | 0 | 0 | 3 984 | -25 000 | -21 016 |
| 1 | -21 016 | -2 102 | 3 984 | 0 | -19 133 |
| 2 | -19 133 | -1 913 | 3 984 | 0 | -17 062 |
| 3 | -17 062 | -1 706 | 3 984 | -500 | -15 285 |
| 4 | -15 285 | -1 528 | 3 984 | -500 | -13 329 |
| 5 | -13 329 | -1 333 | 3 984 | -500 | -11 178 |
| 6 | -11 178 | -1 118 | 3 984 | -1 000 | -9 311 |
| 7 | -9 311 | -931 | 3 984 | -1 000 | -7 258 |
| 8 | -7 258 | -726 | 3 984 | 4 000 | 0 |
The form of presentation may appear unconventional. The figure trial contribution is
the solution, but it appears at the top of the spreadsheet. This is the nature of
iteration; we start with a guesstimate of the solution and then progressively refine it.
It yields te same figure as the other method, but with a lot less pain and uncertainty,
and with less risk of error, for this form of presentation is self-checking.
The particular example shown is trivial, in that it yields a result with very little variation between the options. (Only the short disposal option is significantly more expensive, reflecting the premium people are willing to pay for a "new" car.) If there is a vigorous and economically rational market operating for used cars, then disposal values should be a function of expected future maintenance costs and expected residual life.
 When there is no
disposal market, however, life cycle costing becomes essential. Many public sector assets
have zero or uncertain disposal value. It is possible, for example, that the government
scraps old military equipment rather than let it find its way to the world used arms
market.
When there is no
disposal market, however, life cycle costing becomes essential. Many public sector assets
have zero or uncertain disposal value. It is possible, for example, that the government
scraps old military equipment rather than let it find its way to the world used arms
market.
An example of a practical policy application of life cycle costing is provided by the ACT Electricity and Water Authority, which has confronted the options for future water supply in Canberra. Basically the options they face are to build one big dam, which would initially provide excess capacity but would provide many years of service, or a series of smaller dams, which would be built incrementally as the need arises. (This was the subject of a seminar presented by Jenelle Kenner, a student at the University of Canberra 1993.) Life cycle costing is the obvious approach to such a problem.
Another example is in housing. Imagine a public housing authority wants to set a
"fair" rent, which exactly covers long run costs. Because different costs occur
over different times in the life of a house, life cycle costing is a means of spreading
costs evenly over time. Similarly with capital works such as pavement maintenance on
roads.
Exercise
Consider an option to buy two general purpose light trucks for the military. The options are shown below.
| Option 1 | Option 2 | |
| Purchase Price ($) | 80 000 | 55 000 |
| Annual Operating Cost ($) | 3 000 | 4 000 |
| Life (years) | 10 | 6 |
Neither truck has any disposal value. The discount rate is 8 percent.
The completed workbook is at ch13ex02.xls, showing both ways of approaching the problem. Also in the workbook is an example of a third approach for ranking these projects, using a 30 year perpetual replacement cycle (the lowest common multiple of 10 and 6). This allows you to rank the projects, but it doesn't give you an annualized cost, which you still have to derive with an annuity formula.
General References
Any good management accounting text will give a description of life cycle costing. A very rigorous approach is in Charles Coe Public Financial Management (Prentice Hall 1989). I am not aware of any text which covers the difference equation method of life cycle costing.