|
|
If all projects could be subject to benefit-cost analysis (rather than the more restrictive process of cost-effectiveness analysis), the decision rule would be to select all projects with positive net benefits. This is simply the application of the fundamental rule.
Would this lead to a flood of projects? No; the process is theoretically self-limiting.
For almost all realistically conceivable projects, their NPV will be dependent on the discount rate. These NPVs will be positive for low discount rates, turning negative when discount rates rise. Imagine a world with a zero discount rate. All sorts of projects would be viable. It may be sensible to duplicate the road from Broken Hill to Bourke, on the basis that the investment will pay itself back over the next hundred years There will be scores of such possible projects (perhaps even a new dam in Queensland). As the discount rate is raised, however, more and more projects flip from positive to negative NPVs. Eventually, at a high enough discount rate, almost no projects would have a positive NPV. (The exceptions may be a few quick projects with immediate benefits.)
As an example, consider a project to improve an intersection on a road. One option is to do nothing. Another is to build a rotary, for $2.0 million, with community savings of $600 000 a year. A third option is to build an interchange for $7.0 million, with community savings of $2 000 000 a year. (A spreadsheet is at ch10ex01.xls showing a one year construction phase and a ten year evaluation.) The decision rule is as follows:
| Low discount rates | both projects have positive NPVs, but interchange has higher NPV than rotary. Build interchange. $7.0 million. |
| Intermediate rates | rotary has positive NPV higher than interchange. Build rotary. $2.0 million. |
| High discount rates | both projects have negative NPVs, Build neither. $0. |
(We will come back to this project when we look at means to rank projects.)
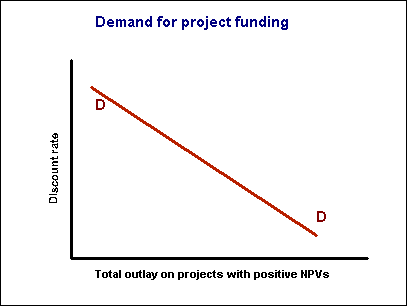Imagine a whole set of possible such projects. We could construct a demand
curve, with the discount rate on the Y axis, and the amount of funding required for those
projects on the X axis. (This adheres to the economists' convention of putting the
independent variable on the Y axis.) The lower the discount rate, the more projects get
up.
This reveals the sensitivity of capital outlays to the discount rate. If the rate is raised, then there will be few projects with positive NPVs, and therefore less demand for capital funding. (That is why monetary policy has such an effect on private and corporate investment.)
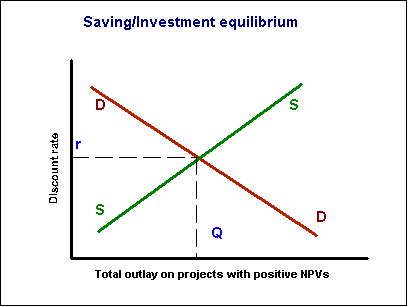
The discount rate, of course, does not come out of the blue. To complete the picture, we can add a supply curve. A higher interest (discount) rate attracts savings; so the supply curve is a conventional upward sloping supply curve. This determines a market discount rate r, and rations capital expenditure to the amount Q. (When governments intervene in the money market using monetary policy, they essentially move the supply curve inwards or outwards, by creating other markets for funds which are more or less attractive to investors.)
Actual Practice
This diversion into classical economic theory shows the most economically rational way of funding projects. It provides a reasonable first order approximation of what happens in the private sector and how monetary policy influences investment.
The public sector often faces capital rationing, however. What is given is not a discount rate, but a capital budget. (See Chapter 2 on the budgetary process.)
The most rational approach would be to have every possible project on one large computer program, and to move the discount rate until the amount of funding just absorbs the capital budget. This tends to favor those projects with the best internal rate of return. This method is generally used in private enterprise. This would ensure that the community would get the highest return for the constrained capital budget. (Even this conventional approach is criticized by John Quiggin, because it depends on using high discount rates to suppress long life projects.(1))
In practice, governments tend not to do this, however. More commonly they set a discount rate, and at any given discount rate there are usually more projects than funding. Therefore some other form of rationing has to be used.
The mathematical approach is to view such a problem as one in operations research. This is known as the backpackers' problem, in recognition of the backpacker having a number of items he or she can carry, all with positive utility, but the total weight is beyond his or her weight limit. What does the backpacker do?
Simple problems of this nature can be solved exhaustively using a process known as integer programming, with appropriate decision rules built in for mutually exclusive or complementary items. (A lightweight tent and a winter tent are mutually exclusive; a sleeping mat and a lightweight bag may be complementary.) Integer programming essentially tests all combinations within the constraint, and generates the solution with the highest utility. Beyond a certain small scale, integer program programming becomes impossible because of the scale of the problem, and a more sophisticated algorithm must be used. (Integer programming with N choices requires evaluating up to N! possible solutions.) The "solution" from an operations research algorithm may not be the optimum, but it will be close to the optimum.
In fact backpackers manage to pack without the aid of a mainframe computer, and some are not even familiar with integer programming. They put in a few essentials, and allocate the remainder by what seems to be heuristic rule of the ratio of utility to weight, until, the weight limit is reached. Chocolates get packed; canned fruit in syrup is left behind.
A similar approach is taken to project funding. One approach is to accept the projects with the highest benefit/cost ratios. This is problematic, however, in that benefit/cost ratios are manipulable, a point taken up in the next section. Another approach is to use the NPV/C ratio, where C is the project's demand on the capital budget. (This is sometimes also called the NPV/K ratio.)
This approach has its limitations, especially for mutually exclusive projects, in that it tends to favor low capital cost approaches, even if they yield smaller NPVs than competing larger projects. The rotary/interchange example illustrates this point, where, at a discount rate of 8.0 percent, the interchange has a much higher NPV, but the rotary has a higher NPV/C ratio.
It is possible that governments fear using a pure capital rationing system (that is,
setting a discount rate just high enough to clear a capital budget), because that could
allocate the whole capital budget to a few large projects. They may prefer the sub-optimal
approach of spreading their largesse. That may explain why road planning tends to appear
haphazard, with a series of half-measures, rather than a few larger projects which get it
right the first time. Indeed, initiatives such as the Federal Government's "black
spot" program deliberately took an approach favoring small projects over systematic
improvements to the road network.
A common approach in ranking projects, or in advocating projects, is to add all the benefits, add all the costs, and express these as a ratio. (The rotary/interchange spreadsheet is a case in point. Benefit/cost ratios can be subject to significant manipulation however. They are not, in themselves, useful for ranking competing projects.
Exercise
A railroad project can return the following annual income and revenue.
| Annual revenue and expenses $ million | |
Expenses |
Revenue |
| Passenger services | |
| 10.0 | 8.0 |
| Freight services | |
| 20.0 | 25.0 |
Show how this project can have a benefit/cost ratio of 1.1 or 2.5. Which is the more
legitimate measure?
Exercise
Congestion, pollution and accidents which result from the Ned Kelly Highway passing through the center of Dead Goanna are estimated to cost, at a discounted present value, $2.0 million. A new by-pass road around the city of Dead Goanna would cost $4.0 million. Another benefit of the road would be a saving in travelling time for travellers on the main road of $3.0 million. Show how this project can have a benefit-cost ratio of 2.0 or 1.25.
Because of the possibility of such manipulation as illustrated in these two exercises,
there is a risk in ranking projects on the basis of benefit-cost ratios alone.
When we have to rely on cost-effectiveness analysis, by definition we cannot bring costs and benefit to a common measure, and no single figure (e.g. NPV) or dimensionless ratio (e.g. benefit-cost ratio) is available. But if we do have a cardinal scale of benefits, and a notion of how those benefits respond to expenditure, we can use an economically rational form of expenditure allocation.
For example, in public health we may be able to evaluate which interventions are most likely to add to life years (or quality adjusted life years, a WHO measure used in cost-effectiveness analysis).
As an example, imagine we have $20 million to spend on cancer prevention, in three programs - early cancer screening, public health promotion, and school promotions. How should we allocate across these programs to produce most QALYs?
Theoretically we should titrate activity and expenditure in each of these areas until the benefits equate at the margin. In any well-managed public health program expenditure will be subject to diminishing marginal benefits - the sixth sunscreen advertisement for 'slip/slap/slop' will be less effective than the fifth advertisement. The extra benefit of a second annual pap smear will not be as great as the initial benefit of one annual pap smear. Therefore we should balance expenditure among the three programs so that the benefit (in terms of QALYs) from the last dollar on each program equates. If, for example, at the margin, we were getting more benefits from our schools program than from the screening program, then we should transfer resources from screening to schools until those benefits balance at the margin. This approach is illustrated in the figure above. Note the downward-sloping marginal benefits (QALYs).
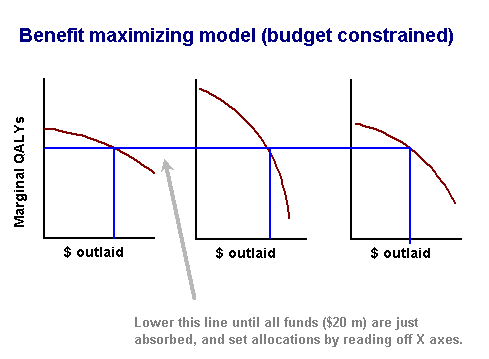
Of course such fine-tuning is difficult. It may be possible to adjust the amount of advertising on health promotion very finely, but our screening program may involve a few large clinics, which involve more than marginal allocations; we either fund them or we don't.
And, as pointed out in Chapter 8, people do not necessarily seek an economically rational approach to such matters. If they did, they would be willing to make tradeoffs in areas like safety regulation, perhaps accepting lower standards of airline safety with the savings redirected to surface transport safety. A problem is that people do not have a consistent approach to risk; people exhibit different degrees of risk aversity in different situations.(2) People may seek complete protection (pseudocertainty) in certain areas of their lives, while being highly exposed in others. For example, many people seek complete insurance cover against fire damaging their house, while being entirely uncovered for flood. Perhaps the most extreme public policy example was the Reagan Administration's proposal for the multi billion dollar Strategic Defense Initiative ("Star Wars"), which would have protected America from airborne intercontinental missiles, but would have been ineffective against a nuclear device floated up the Hudson River on a barge.
All the foregoing assumes that choosing alternative projects is a smooth, low-cost exercise. That is not the case. Usually only a limited range of options is evaluated, and the project briefs are, in themselves, limited, Errors in planning rarely lie in the techniques of project evaluation; rather they lie in two other areas:
Poor policy coordination - agencies often fail to see the interrelationship of policies. An education authority may close schools, looking only at the economies of school operation, without looking at the extra transport demands.
A failure to examine assumptions - agencies often assume past trends will continue. For example, many planners still see transport tasks in terms of moving masses of people at set times between dormitory suburbs and CBDs, even though this pattern of commuting is already on the wane.
This is not the place to go into these other planning problems. But it is as well to remember that no amount of financial or computing sophistication will compensate for inadequate attention to planning assumptions.
Finally, benefit-cost studies are expensive. The mathematical manipulations are easy; spreadsheets have overcome the number crunching problems. But data collection is expensive, especially when it comes to approaches such as contingent valuation. That is the ultimate constraint on such analytic techniques.
1. John Quiggin Short Term Bias and Australia's Economic Performance (Paper delivered to EPAC Seminar 10 November 1994)
2. Max Bazerman Judgement in Managerial Decision Making (John Wiley & Sons 1986)
